Cluster Organization
In the case of a distributed system, the key element is communication between processes. This dictates the system's performance, fault tolerance, and the logic of information transfer flow between nodes within the distributed system.
From an architectural point of view, nodes can be organized in several ways within a cluster:
- grid → nodes are organized in levels. Each node can communicate with neighbors horizontally and vertically. The flow of information is both vertical and horizontal. Each node has a maximum of 4 neighbors.
- ring → nodes are organized in a circle. Each node communicates with neighbors to the left and right. The flow of information is horizontal. Each node has two neighbors.
- tree → nodes are organized hierarchically in a tree-like structure. The flow of information is vertical. Each node can have an unlimited number of neighbors.
- graph → nodes are organized in a graph-like structure. Each node can communicate with one or more neighbors. The flow of information is abstract. Each node can have an unlimited number of neighbors.
In this laboratory, we will explore the organization of a system in the form of a generic graph. The topology below will be used for explanations in the laboratory and exercises.
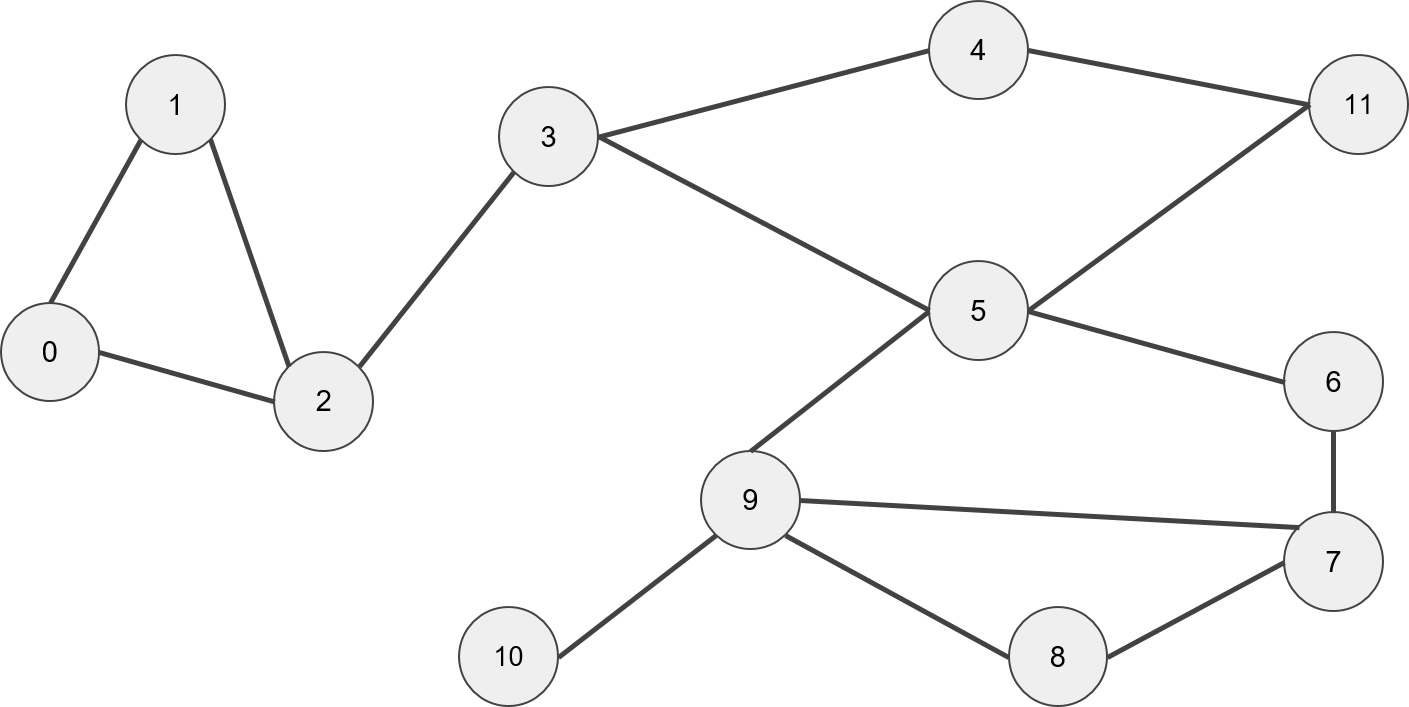
Establishing Topology
There are three ways in which a topology can be established within a cluster. Nodes can either know the state of the entire cluster from the beginning, know only their neighbors, or know nothing about the system's state.
To establish the topology, the cluster can operate in two ways:
- nodes can transmit their state to other nodes multiple times until all nodes have the topology established. The number of times needed to ensure topology between nodes is called convergence. This mode is simple to implement but inefficient.
- nodes choose a leader to calculate the system's topology.
The problem that arises when using a leader to create the topology matrix is that nodes do not know the path to the leader, only who the leader is. The covering tree solves this problem. Based on the covering tree, nodes send the information they have to the leader, passing through intermediate nodes represented by their parents in the tree. Intermediate nodes add the received information to their own and pass it on. In the end, the leader has all the system's information and can create the topology matrix. The matrix is then sent to each node individually.
In this laboratory, we will explore establishing topology through leader selection.
In the case of computer networks, routers and switches are organized in the form of a cluster where nodes initially know nothing about the system's state.
In the case of leader selection, it is not necessary to know the topology at the beginning, only the neighbors with which nodes can interact.