Odd-Even Transposition Sort (OETS)

One of the most well-known (though not necessarily efficient) sorting algorithms is bubble sort. It operates based on the following pseudocode:

function bubbleSort(list) {
  sorted = false;
  while (!sorted) {
    sorted = true;
    for (var i = 0; i < list.length - 1; i++) {
      if (list[i] > list[i + 1]) {
        swap(list[i], list[i + 1]);
        sorted = false;
      }
    }
  }
}

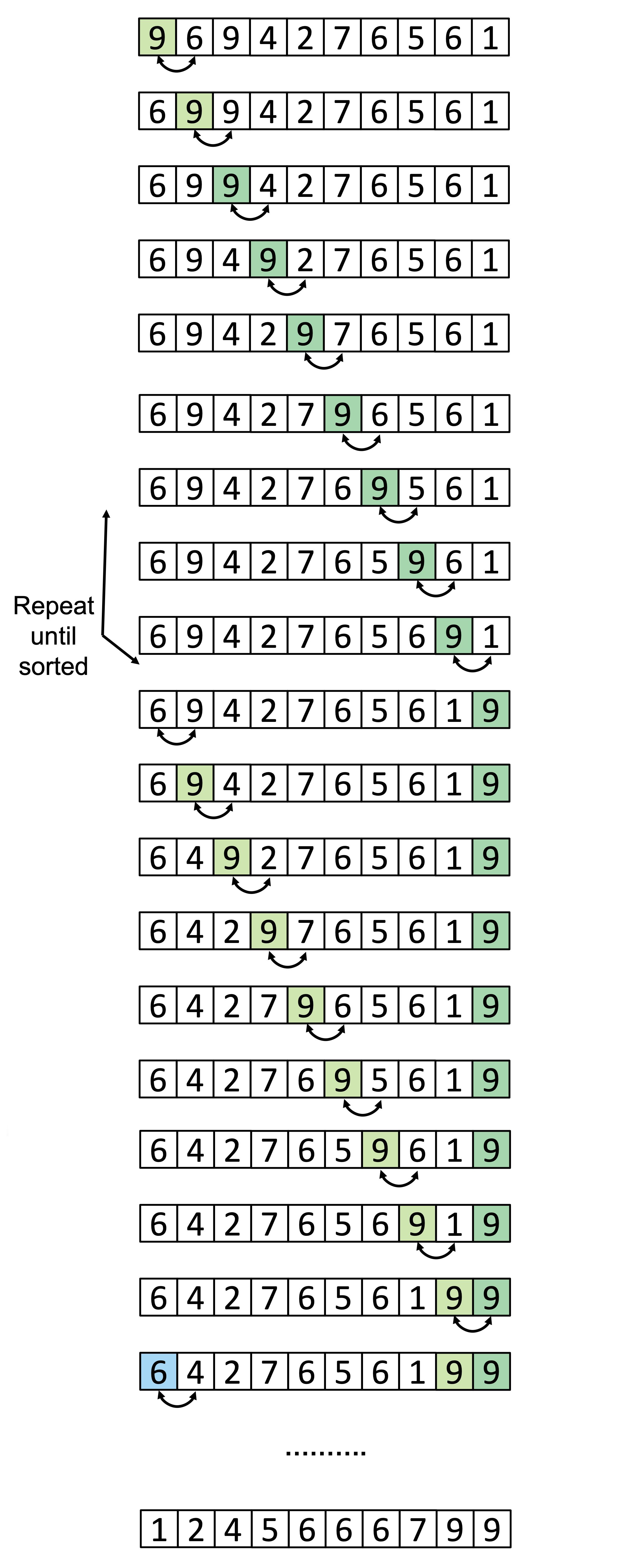
As can be seen above, bubble sort traverses the array to be sorted element by element, comparing the current element with its right neighbor. If the number on the right is smaller, a swap is made between the current element and the one on its right. The complexity of this algorithm is O(N²), as it finishes in at most N iterations of the array (where N is the number of elements in the array to be sorted).

An example of the behavior of bubble sort can be seen in the image below.

If we wanted to parallelize this algorithm, a potential approach would be to perform the comparison and potential swapping of neighboring elements in parallel. However, this could lead to the problem depicted in the image below.

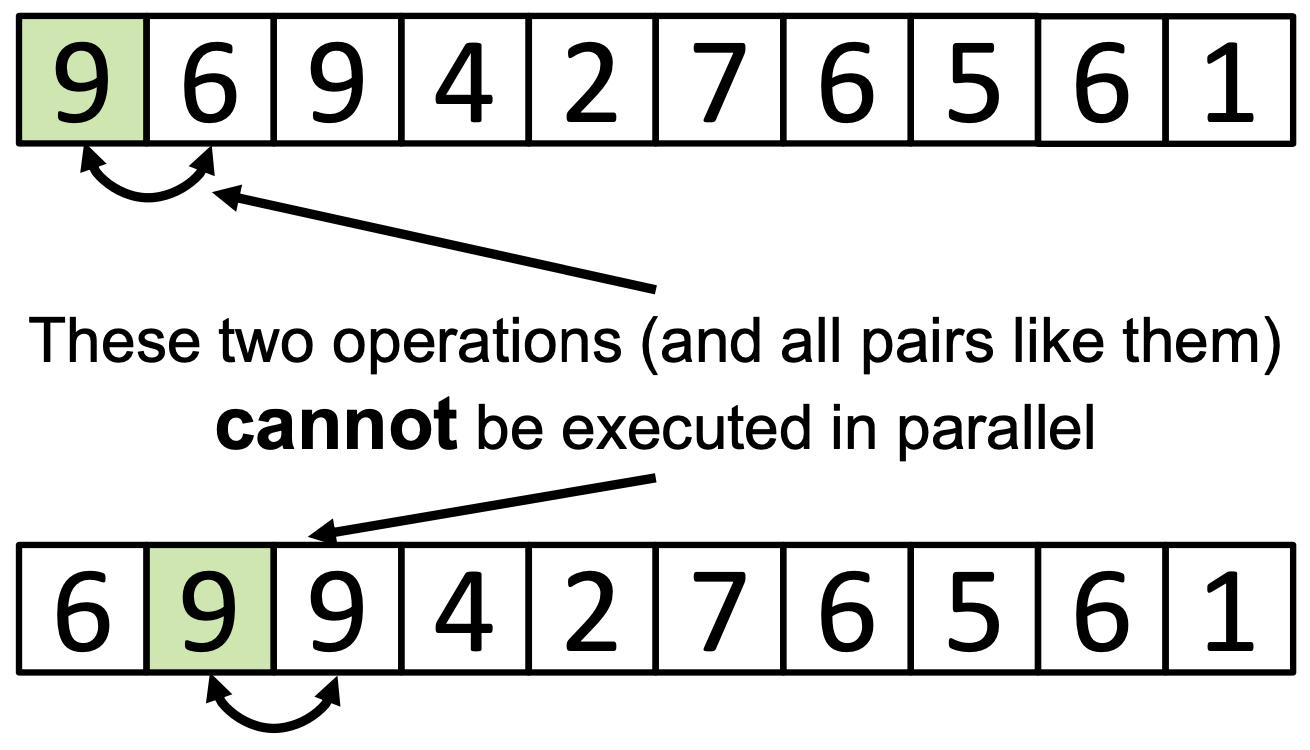
More precisely, operations on adjacent elements cannot be performed simultaneously because it could lead to a race condition. For this reason, one way to parallelize bubble sort is given by the odd-even transposition sort algorithm, which operates according to the following pseudocode:

function oddEvenSort(list) {
  for (var k = 0; k < list.length; k++) {
    for (i = 0; i < list.length - 1; i += 2) {
      if (list[i] > list[i + 1]) {
        swap(list[i], list[i + 1]);
      }
    }
    for (i = 1; i < list.length - 1; i += 2) {
      if (list[i] > list[i + 1]) {
        swap(list[i], list[i + 1]);
      }
    }
  }
}

As can be seen above, odd-even transposition sort has two phases. In the even phase, the elements at even positions in the array to be sorted are compared (and possibly swapped) with their neighbors on the right. After the even phase is complete (i.e., after all even elements have been processed), the odd phase follows, in which odd elements are examined and compared with their neighbors on the right. Similar to bubble sort, the maximum number of iterations required to sort an array will be N (the number of elements in the array). If we have P threads of execution, the complexity of this algorithm will be O(N/P*N), or O(N) for P=N. In the image below, you can see a graphical representation of how odd-even transposition sort works.

tip

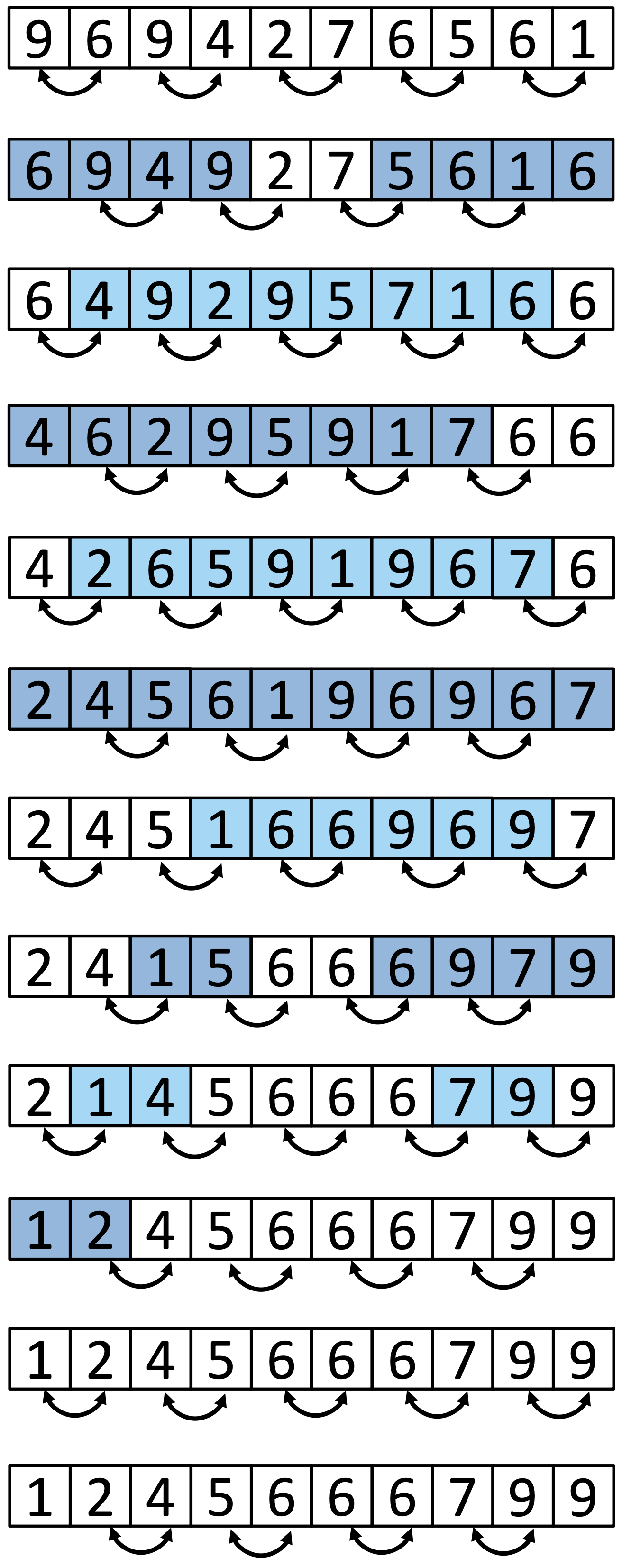
The odd-even transposition sort algorithm was originally designed to run on processor arrays, where each processor holds a single value from the array to be sorted and can only communicate with the processor to the left and the one to the right.