Odd-even transposition sort (OETS)

Unul din cei mai cunoscuți (chiar dacă nu neapărat eficienți) algoritmi de sortare este bubble sort. Acesta funcționează pe baza următorului pseudocod:

function bubbleSort(list) {
  sorted = false;
  while (!sorted) {
    sorted = true;
    for (var i = 0; i < list.length - 1; i++) {
      if (list[i] > list[i + 1]) {
        swap(list[i], list[i + 1]);
        sorted = false;
      }
    }
  }
}

Așa cum se poate observa mai sus, bubble sort parcurge șirul de sortat element cu element, comparând elementul curent cu vecinul din dreapta. Dacă numărul din dreapta este mai mic, se realizează o interschimbare între elementul curent și cel din dreapta sa. Complexitatea acestui algoritm este O(N²), pentru că se termină în cel mult N parcurgeri ale șirului (unde N este numărul de elemente din șirul de sortat).

Un exemplu de comportament al bubble sort se poate observa în imaginea de mai jos.

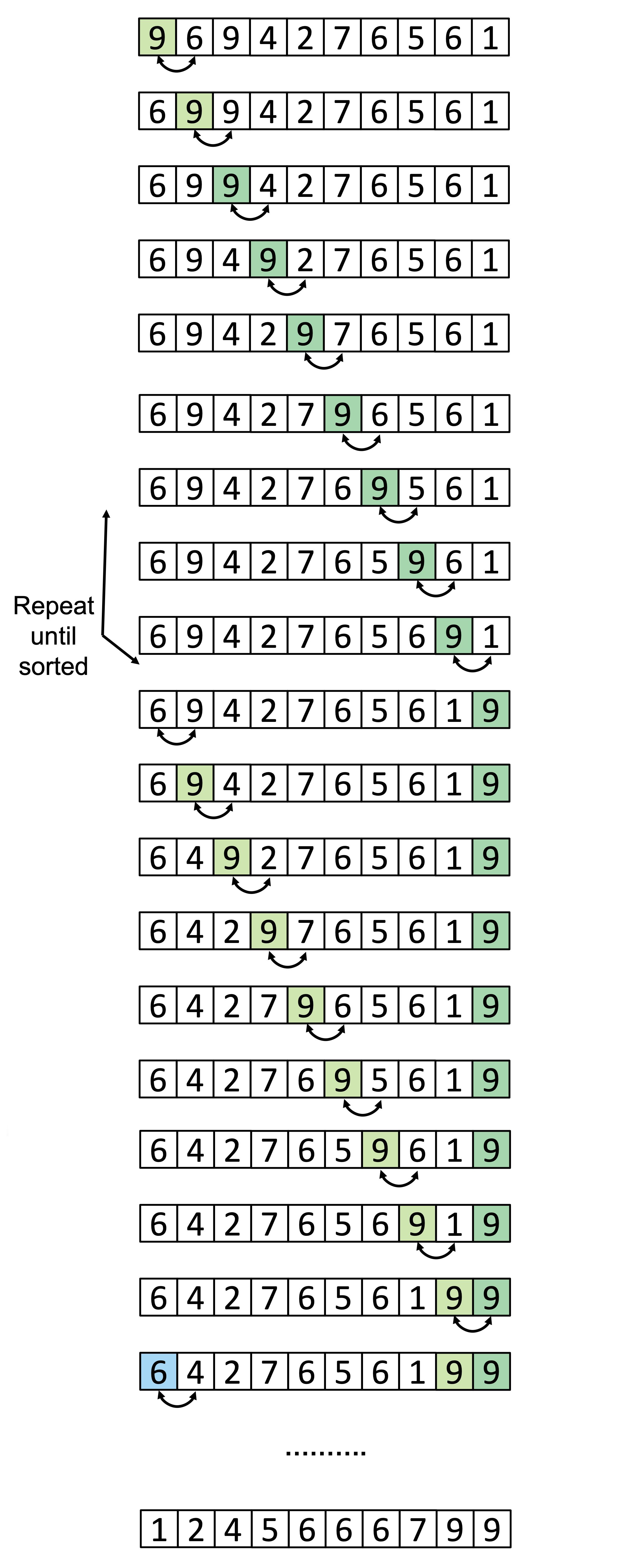
Dacă am dori să paralelizăm acest algoritm, un potențial mod de abordare ar fi să realizăm în paralel comparația și potențiala interschimbare de elemente vecine, dar acest lucru ar putea duce la problema prezentată în imaginea de mai jos.

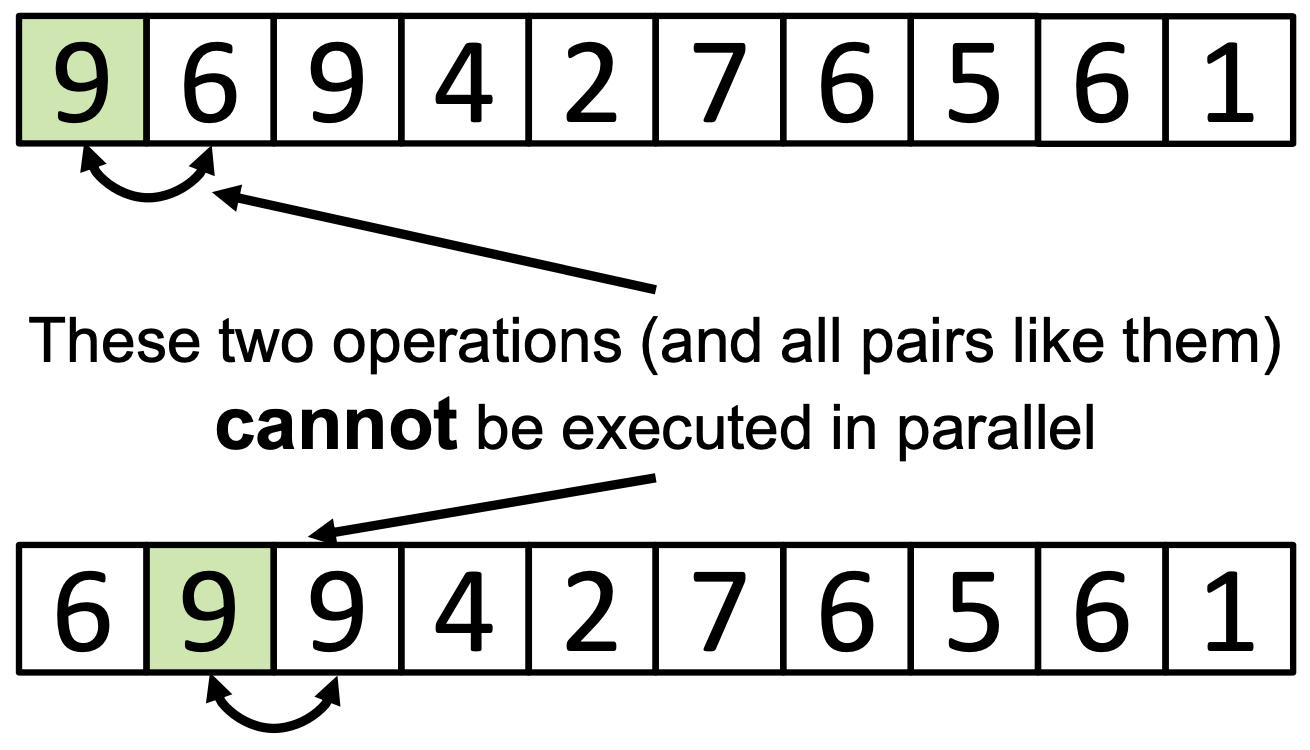
Mai precis, operații pe elemente adiacente nu se pot realiza simultan, pentru că se poate ajunge la un race condition. Din acest motiv, un mod de a paraleliza bubble sort este dat de algoritmul odd-even transposition sort, care funcționează după următorul pseudocod:

function oddEvenSort(list) {
  for (var k = 0; k < list.length; k++) {
    for (i = 0; i < list.length - 1; i += 2) {
      if (list[i] > list[i + 1]) {
        swap(list[i], list[i + 1]);
      }
    }
    for (i = 1; i < list.length - 1; i += 2) {
      if (list[i] > list[i + 1]) {
        swap(list[i], list[i + 1]);
      }
    }
  }
}

Așa cum se poate observa mai sus, odd-even transposition sort are două faze. În faza pară, elementele de pe poziții pare din șirul de sortat sunt comparate (și eventual interschimbate) cu vecinii din dreapta. După ce se termină faza pară (adică după ce toate elementele pare au fost procesate), urmează faza impară, în care elementele impare sunt analizate și comparate cu vecinii din dreapta. La fel ca la bubble sort, numărul maxim de iterații necesare pentru a sorta un șir va fi N (numărul de elemente din șir). Dacă avem P fire de execuție, complexitatea acestui algoritm va fi O(N/P*N), sau O(N) pentru P=N. În imaginea de mai jos, se poate observa o reprezentare grafică a modului de funcționare al odd-even transposition sort.

sugestie

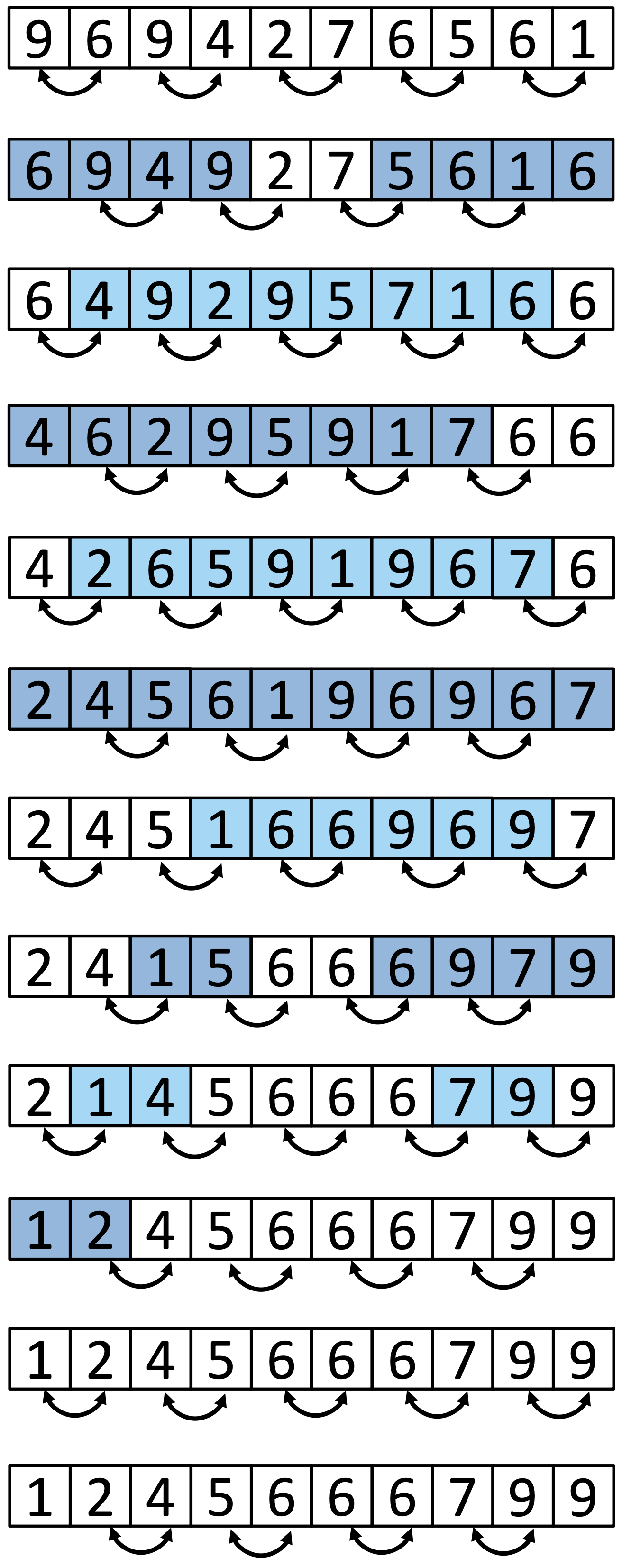
Algoritmul odd-even transposition sort a fost gândit inițial pentru a fi rulat pe șiruri de procesoare (processor arrays), unde un procesor conține o singură valoare din șirul de sortat și poate comunica doar cu procesorul din stânga și cu cel din dreapta.